In part one of this mini-series I talked about where statements like “this poll is considered accurate within 3 percentage points” come from and how it is possible that this is not at odds with the observed variability in the many polling results. For convenience let’s reconsider just how variable these polls are.
A mid-November Ipsos Reid poll has Chow at 36 percent, Tory 28 percent, Ford 20 percent, Stintz 13 percent, Soknacki 3 percent, undecided 0 percent. While in late February, a Forum Research poll has Chow at 31 percent, Tory 27 percent, Ford 31 percent, Stintz 6 percent, Soknacki 2 percent, Undecided 3 percent. Summarized in a table we have the following data.
| Individual | Ipsos Reid | Forum Research |
|---|---|---|
| Olivia Chow | 36% | 31% |
| Rob Ford | 20% | 31% |
| John Tory | 28% | 27% |
| Karen Stintz | 13% | 6% |
| David Soknacki | 3% | 2% |
| Undecided | 0% | 3% |
In part 1, I mentioned that what is really being measured in each one of these polls is not the support of the candidate by the whole population, but rather the support of the candidate by those that have been polled. If we suppose that the Ipsos Reid values represent the true distribution and that the Forum Research values are uncorrected due to an insufficient representation of individuals without a landline then a very interesting question to pose is
what is the voting distribution of this unpolled population?
Although much has happened in the intervening period, from mid-November to late February, I will assume that the underlying voting distribution of the population has remained essentially the same. Recall the recipe from part 1 to find the true proportion for a given candidate that
\[
P(\textrm{candidate}) = P(\textrm{candidate}|\textrm{has landline})P(\textrm{landline})+P(\textrm{candidate}|\textrm{no landline})P(\textrm{no landline}).
\]
(English translation: The probability of support for a candidate is the probability they are supported by an individual with a landline weighted by the probability of having a landline together with the support by an individual without a landline weighted by the probability of not having a landline.) With our suppositions, the ingredients to the recipe differ than what we had in part 1. For part 2 they are as follows:
- \(P(\textrm{candidate}|\textrm{has landline})\) is the uncorrected (Forum Research) values in the table for a given candidate;
- \(P(\textrm{candidate}|\textrm{no landline})\) is unknown proportion that we are attempting to extract;
- \(P(\textrm{landline}) = p\) is taken as a variable \( 0 \le p \le 1\) and from the discussion in part 1, \(p\) is becoming smaller over time and is expected to be less than 0.67 in 2014;
- \(P(\textrm{no landline}) = 1-p\) depends on the value of \(p\).
This gives 6 equations (one for each candidate) in seven variables so the solution has a single parameter which we choose to be \(p\). Denoting \(\alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5, \alpha_6\) as the probabilities of support, for those without a landline, for each of the candidates: Chow, Ford, Tory, Stintz, Soknacki, and undecided respectively, then a naive attempt is to simultaneously solve
\begin{align*}
0.36 &= 0.31p + \alpha_1(1-p)\\
0.20 &= 0.31p + \alpha_2(1-p)\\
0.28 &= 0.27p + \alpha_3(1-p)\\
0.13 &= 0.06p + \alpha_4(1-p)\\
0.03 &= 0.02p + \alpha_5(1-p)\\
0 &= 0.03p + \alpha_6(1-p)
\end{align*}for each \(\alpha_i\). Not all solutions are valid since we would like \(0\le p\le 1\) and \(0 \le \alpha_i\le 1\) for \(i = 1,2,\ldots,6\). With this constraints in place, the only solution is to set \(p=0\) corresponding to everyone having only a cell phone. In this degenerate case, the unobserved distribution is simply what the Ipsos Reid data indicates and the Forum Research results play no role. Essentially this degenerate solution is a result of asking for an exact match between the two polls.
The details of how I solved this problem (for the mathies) can be found elsewhere. For everyone else, let me tell you the solution. First we move from looking for an exact result to looking for a result that most closely matches the two polls while still observing all the constraints. The figure summarizes the results and there are two very interesting scenarios that show up.
| Individual | Ipsos Reid | Forum Research | \(p=76.2\%\) | \(p=63.3\%\) |
|---|---|---|---|---|
| Olivia Chow | 36% | 31% | 45.8% | 43.6% |
| Rob Ford | 20% | 31% | 0% | 0% |
| John Tory | 28% | 27% | 25.0% | 28.7% |
| Karen Stintz | 13% | 6% | 29.2% | 24.0% |
| David Soknacki | 3% | 2% | 0% | 3.7% |
| Undecided | 0% | 3% | 0% | 0% |
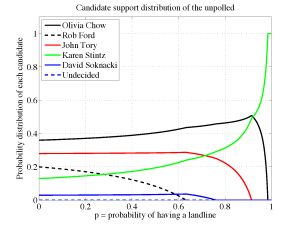
If we suppose that \(p=76.2\%\) of people are represented by a landline then the voting distribution of the non-polled that best approximates the Ipsos Reid results when combined with the Forum Research data is: Chow at 45.8 percent, Tory 25.0 percent, Ford 0 percent, Stintz 29.2 percent, Soknacki 0 percent, Undecided 0 percent. We suspect though that \(p\) is actually lower than this and taking \(p=63.3\%\) gives a slightly different result of: Chow at 43.6 percent, Tory 28.7 percent, Ford 0 percent, Stintz 24.0 percent, Soknacki 3.7 percent, Undecided 0 percent.
I was personally very surprised that there is no support at all for Rob Ford from the non-polled provided that \(p \ge 63.3\%\). I would have expected there to be some small residual but this is simply not borne out of the analysis. Of course for lower values of \(p\) (\(p < 63.3\%\)) support is found for Rob Ford but it is curious that this support is systematically included in the Forum Research data and not found at all within the optimal distribution of the non-polled until \(p\) is quite low. Furthermore, a low value of \(p\) simply confirms an inappropriate bias towards those with landlines in the Forum Research values. What does this mean? Well first, take the polling results with a grain of salt and second, it's fairly clear that the voting distribution of those with a landline and without a landline are significantly different especially concerning Rob Ford, Karen Stintz and Olivia Chow. The reduction in the Ford proportion in the non-polled is effectively evenly split between Stintz and Chow. Rob Ford in particular may have a Karl Rove moment where the numbers simply do not support the hype within the campaign bubbles. To those in the non-polled, get out and vote, your voice is clearly not being represented and is an integral part of the future of Toronto. Now let’s see how this optimal distribution could be found.