Continuity
A function \(f(x)\) is said to be continuous at a point \(a\) in its domain if the following three properties hold.
- \(\displaystyle \lim_{x \to a} f(x)\) exists. This takes three steps to show in itself.
- \(f(a)\) has to exist,
- \(\displaystyle \lim_{x \to a} f(x) = f(a)\).
Continuity connects the behaviour of a function in a neighbourhood of a point with the value at the point.
If the domain of the function is bounded say \([a,b]\) then each end point of the interval can only be approached in one way. The left end point is at \(x = a\) so \(f(x)\) is said to be continuous at the left end point ‘\(a\)’ if \(\displaystyle \lim_{x \to a^+} f(x) = f(a)\). In a similar fashion, \(f(x)\) is said to be continuous at the right end point ‘\(b\)’ if \(\displaystyle \lim_{x \to b^-} f(x) = f(b)\).
Types of Discontinuities
Since there are only a few ways that the limit of a function cannot exist at a point there are few ways that a function can fail to be continuous. These are classified into four types.
1. Jump Discontinuity (also known as a simple discontinuity)
2. Removable Discontinuity
3. Infinite Discontinuity
4. Oscillatory Discontinuity
An explicit example of each type of discontinuity follows next.
Examples
1. Jump Discontinuity:

Is \(
f(x) = \begin{cases}
\displaystyle x-1, & 1 \le x \le 2 \\
-1, & -2 \le x < 1
\end{cases}
\) continuous at \(x = 1\)? Where is \(f(x)\) continuous?
To answer this we go back to the definition. By computing \(L^+ = 0\) and \(L^- = -1\) (for \(x = 1\)) we see that they are not equal and consequently, \(\displaystyle \lim_{x \to 1} f(x)\) DNE. Therefore \(f(x)\) is not continuous at \(x=1\). As to where \(f(x)\) is continuous, this is everywhere else in the domain \((-2,1) \cup (1,2)\). For the endpoints, in this case we say that \(f(x)\) is continuous from the right at \(x=-2\) and continuous from the left at \(x=2\).
A graph of the function appears to the right.
2. Removable Discontinuity:
Consider \(
g(x) = \begin{cases}
\displaystyle x, & x \ne 2 \\
5, & x = 2.
\end{cases}
\) Is \(g(x)\) continuous at \(x = 2\)? No because even though \(\displaystyle \lim_{x\to 2}g(x) = 2\) exists, \(\displaystyle \lim_{x\to 2}g(x) \ne g(2) = 5\). Since this function can be made continuous by redefining it at \(x=2\), we call this type of discontinuity removable.
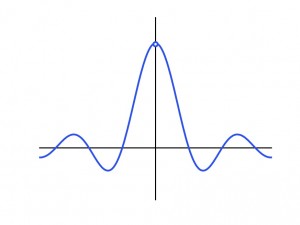
To illustrate how a function can be fixed, notice that \(
f_1(x) = \displaystyle\frac{\sin x}{x}
\) is not continuous for all \(x\in {\Bbb R}\) since \(f_1(0)\) DNE. However, \(
f_2(x) = \begin{cases}
\displaystyle \frac{\sin x}{x}, & x \ne 0 \\[3mm]
1, & x = 0
\end{cases}
\) is continuous for all \(x\in {\Bbb R}\).
3. Infinite Discontinuity: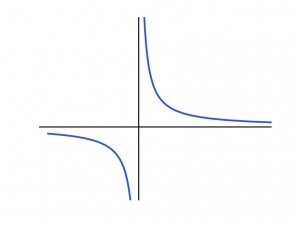
Consider the function \(y = 1/x\) on any domain that includes \(x=0\). Since the function becomes unbounded continuity fails at \(x=0\) since the limit does not exist there. The domain of the function is very important since the same function on a different domain (\(\displaystyle y = 1/x, 1 \le x \le 2\)), does not have an infinite discontinuity because it does not become unbounded on the given domain.
4. Oscillatory Discontinuity:
This type of discontinuity occurs when a function oscillates too much, as in the case of \(y = \sin(1/x)\). As \(x\to 0\), \(f(x)\) does not approach a single value.
 We leave it as an exercise to the student to show that
We leave it as an exercise to the student to show that
\( f(x) = \begin{cases}
\displaystyle x\sin\left(\frac{1}{x}\right), & x \ne 0 \\[3mm]
0, & x = 0
\end{cases}
\) is a continuous function for all \(x\in {\Bbb R}\).
🙂 There are many other ways a function can be discontinuous.
The list of discontinuities should be sufficient for nice functions (i.e., “elementary” functions aka closed form expressions involving polynomials, trig, log, etc.).