Introduction to Limits
The limit of a function is concerned with the behaviour of a function near a given point. What happens at the point is of no concern. To be more precise,
if “the limit of the function \(f(x)\) as \(x\) approaches the point \(a\)” is the value \(L\) then this is denoted as\[
\lim_{x\to a}f(x) = L.
\]
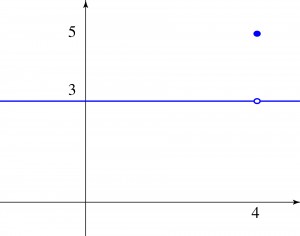
Consider the graph to the right where\[
f(x) = \left\{ \begin{array}{ll}
3, & x \ne 4 \\
5, & x = 4.
\end{array} \right.
\]What is \(\displaystyle\lim_{x\to 4}f(x)\)? There are two ways to approach \(x=4\). From the left and from the right. From the left the limit is \(3\) and from the right the limit is \(3\). Since these limits from the left and right are the same, we can say that\[
\lim_{x\to 4}f(x) = 3.
\]
Note that the limit has nothing to do with what happens at \(x=4\) since \(f(4) = 5\) which is not equal to \(\displaystyle\lim_{x\to 4}f(x) = 3\).
Graphical Way of Looking at Limits
 Now consider the graph to the left. What is \(\displaystyle\lim_{x \to 3} f(x)\)? One can approach this point two ways. From the left, \(\displaystyle\lim_{x \to 3^-} f(x) = 1\) and from the right \(\displaystyle\lim_{x \to 3^+} f(x) = 4\).
Now consider the graph to the left. What is \(\displaystyle\lim_{x \to 3} f(x)\)? One can approach this point two ways. From the left, \(\displaystyle\lim_{x \to 3^-} f(x) = 1\) and from the right \(\displaystyle\lim_{x \to 3^+} f(x) = 4\).
In this example the limit does not exist (DNE) because the limit we get as we approach \(x=3\) depends on the direction in which we approach \(x=3\).
Because of this problem of obtaining a different limit based on the direction in which we approach a point we need the concept of left and right hand limits.
Right and Left Hand Limits
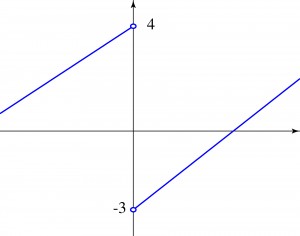
Notice that \(\lim_{x \to 0} f(x)\) DNE. Therefore, the limit you get depends on how you approach \(x = 0\).
As you approach from the left (also called `from below’) \(\lim_{x \to 0^-} f(x) = 4 = L^-\).
As you approach from the right (also called `from above’) \(\displaystyle \lim_{x \to 0^+} f(x) = -3 = L^+\).
In order for the limit to exist at a point, we first require that both the left and right hand limits must exist. By this we mean that both \(L^+\) and \(L^-\) are finite numbers. Second, we require that these values are the same, \(L^+ = L^-\).
We can summarize these ideas in the following theorem.
Theorem 1.1 We say that the limit of \(f(x)\) as \(x\) approaches \(a\) exists and equals \(L\), denoted as \(\displaystyle\lim_{x\to a} f(x) = L\)
1. if \(\displaystyle \lim_{x \to a^-} f(x) = L^-\) exists,
2. \(\displaystyle \lim_{x \to a^+} f(x) = L^+\) exists,
3. and \(L^+ = L^- = L\).
Note that both \(L^+\) and \(L^-\) must exist and not be \(\pm\infty\).