Limits Involving Infinity
Let’s start with what we mean when we say \(\displaystyle \lim_{x \to\infty} f(x) = L\) or \(\displaystyle \lim_{x \to-\infty} f(x) = L\).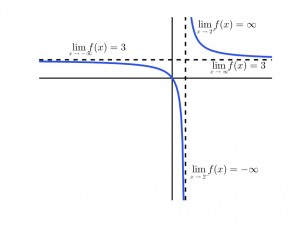
We say \(f(x)\) has limit \(L\) as \(x\) approaches infinity (\(\infty\)) and write \(\displaystyle \lim_{x \to\infty} f(x) = L\) if as \(x\) moves increasingly far from the origin in the positive direction, \(f\) gets arbitrarily close to \(L\).
In an analogous fashion, we say \(f(x)\) has limit \(L\) as \(x\) approaches minus infinity (\(-\infty\)) and write \(\displaystyle \lim_{x \to -\infty} f(x) = L\) if as \(x\) moves increasingly from the origin in the negative direction, \(f\) gets arbitrarily close to \(L\).
Horizontal and Vertical Asymptotes
There are essentially two ways in which infinity can be involved with a given function \(f(x)\). We can either ask how the function behaves if \(x\to\pm\infty\) or find values of \(x\) where the function itself becomes arbitrarily large. The former question deals with finding horizontal asymptotes while the latter question deals with vertical asymptotes.
- We say the function $f(x)\) has a horizontal (like the horizon) asymptote \(y = L\) if either \(\displaystyle \lim_{x \to \infty} f(x) = L\) or \(\displaystyle \lim_{x \to -\infty} f(x) = L\).
- We say the function \(f(x)\) has a vertical asymptote at \(x = a\) if either \(\displaystyle \lim_{x \to a^+} f(x) = \pm \infty\) or \(\displaystyle \lim_{x \to a^-} f(x) = \pm \infty\).
Example:
1. Determine the asymptotes of the function
\[
f(x) = \left\{ \begin{array}{ll}
\displaystyle \frac{1}{(x-1)^2}, & x \ge 0 \\
\displaystyle \frac{x+1}{x}, & x < 0.
\end{array} \right.
\]
This example is little tricky in the sense that the function is defined piecewise and as a result there are two separate horizontal asymptotes.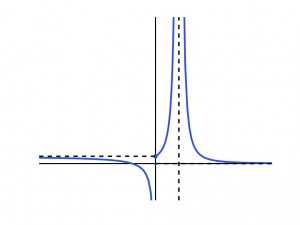
Focusing on the branch for \(x \ge 0\), there is a vertical asymptote at \(x=1\) and since \(\displaystyle \lim_{x\to\infty}f(x) = 0\) there is a horizontal asymptote of \(y = 0\).
For the other branch, \(\displaystyle \lim_{x\to -\infty}f(x) = 1\) giving a horizontal asymptote of \(y = 1\). There is one final vertical asymptote at \(x=0\) since \(\displaystyle \lim_{x\to 0^-}f(x) = -\infty\). The final graph is to the right. Note that the horizontal asymptote \(y=0\) is shown slightly above the line \(y=0\) for clarity.
Oblique Asymptotes
An oblique asymptote describes the situation when the limiting behaviour of the function is a line. One particular way that this can happen is with a rational polynomial \(f(x) = P(x)/Q(x)\) with the \(\mbox{deg }P = \mbox{deg } Q+1\). In this case the asymptote is neither horizontal nor vertical but rather occurs at an angle.
Determining the horizontal, vertical and oblique asymptotes places constraints on the behaviour of the function. This will be illustrated in the example that follow.
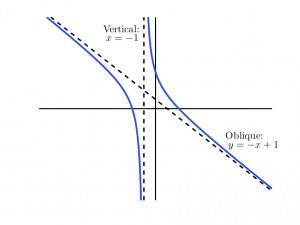Example:
2. Determine the asymptotes of the function \(\displaystyle f(x) = \frac{4-x^{2}}{x+1}\). First of all, there are no horizontal asymptotes since \(\displaystyle \lim_{x\to\pm\infty}f(x) = \mp\infty\). There is a vertical asymptote at \(x = -1\) since \(f(x)\) becomes arbitrarily large at this value. In addition we have an oblique asymptote of \(y = -x+1\) which is found using long division since
\[
\frac{4-x^{2}}{x+1} = -x + 1 + \frac{3}{x+1}.
\]