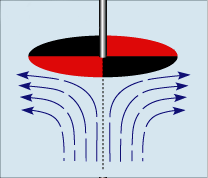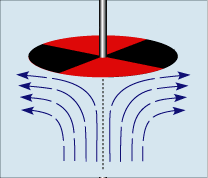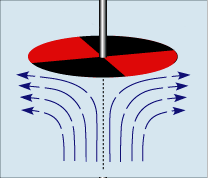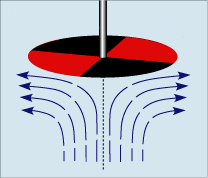
Shown here is a schematic of the rotating disk and how the fluid underneath it moves in response. Notice that the flow near the disk is essentially thrown out to the sides while away from the disk the fluid is effectively pumped towards the disk. There are essentially two separate processes in play here. Far from the disk the flow is essentially upwards towards the spinning sample and near the disk is ejected outward in a thin layer. To get some quantitative idea as to the size of the various terms in the previous expressions we consider a disk of radius \(R\) spinning at angular speed \(\omega\) above a column of fluid of height \(H\). This gives the natural scalings of \(r \sim O(R), z \sim O(H), u_r \sim O(\omega R), u_{\theta} \sim O(\omega R)\). From the continuity equation in Part 1, we see that \(u_z \sim O(\omega H)\) and for the pressure it is scaled to balance the inertial terms yielding \(P \sim O(\rho\omega^2X^2)\) where \(X\) will be determined.
Under these scalings, the equations in Part 1 become
$$\begin{align}u_{r}\frac{\partial u_{r}}{\partial r} -\frac{u_\theta^2}{r} + u_{z}\frac{\partial u_{r}}{\partial z}&=-\frac{X^2}{R^2}\frac{\partial P}{\partial r}+\frac{\mu}{\rho\omega R^2}\left(\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u_{r}}{\partial r}\right) – \frac{u_{r}}{r^{2}}\right) + \frac{\mu}{\rho\omega H^2}\frac{\partial^2u_{r}}{\partial z^2},\\u_{r}\frac{\partial u_{\theta}}{\partial r} + \frac{u_{\theta}u_{r}}{r} + u_{z}\frac{\partial u_{\theta}}{\partial z}&=\frac{\mu}{\rho\omega R^2}\left(\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u_{\theta}}{\partial r}\right) – \frac{u_{\theta}}{r^{2}}\right) + \frac{\mu}{\rho\omega H^2}\frac{\partial^2u_{\theta}}{\partial z^2},\\u_{r}\frac{\partial u_{z}}{\partial r} + u_{z}\frac{\partial u_{z}}{\partial z}&=-\frac{X^2}{H^2}\frac{\partial P}{\partial z} + \frac{\mu}{\rho\omega R^2}\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u_{z}}{\partial r}\right)+ \frac{\mu}{\rho\omega H^2}\frac{\partial^2u_{z}}{\partial z^2}.\end{align}$$
The chemical reactions are going on in the layer just below the rotating disk so this suggests that we should be considering a depth \(H\) on the order of the thickness of the viscous boundary layer so that \(H^2 = \mu/\rho\omega\). The term
$$\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u_{i}}{\partial r}\right) – \frac{u_{i}}{r^{2}}$$
with \(i = r,\theta\) suggest that \(u_r = r f(z)\) and \(u_{\theta} = r g(z)\) and the continuity equation then implies that \(u_z = h(z)\) giving the system
$$\begin{align}f^2-g^2+f’g &= -\frac{X^2}{R^2}\frac{1}{r}\frac{\partial P}{\partial r} + f^{\prime\prime},\\ 2fg + g’h &= g^{\prime\prime},\\ h’h &= -\frac{X^2}{H^2}\frac{\partial P}{\partial z} + h^{\prime\prime},\\ 2f + h’ &= 0.\end{align}$$
Setting \(X=R\) implies from the third expression that \(\partial P/\partial z = 0\) is the dominant effect and from the first equation \(P = Cr^2\) reminiscent of the surface of a rotating bucket. The point here is that this decouples the axial variation in pressure from the axial velocity. If one instead sets \(X=H\) then the axial velocity and pressure variations are connected no matter how fast the disk rotates and at very high rates of rotation \(H^2 \ll R^2\) suppressing the any radial variations in pressure.
This leaves the system of equations for the velocity in the boundary layer under the rotating disk as obtained by von Karman and used by Levich
$$\begin{align}f^{\prime\prime} &= f^2-g^2+f’g,& f(0)&=0, \quad \lim_{z\to\infty}f(z) = 0, \\ g^{\prime\prime} &= 2fg + g’h,& g(0)&=1, \quad \lim_{z\to\infty}g(z) = 0, \\ h^{\prime\prime} &= h’h + p’,& h(0)&=0, \quad \lim_{z\to\infty}h(z) = -\alpha, \\ 2f + h’ &= 0\end{align}$$
enforcing the boundary conditions that i) the fluid in contact with the disk moves with it and ii) outside the boundary layer the velocity is essentially upwards independent of radius.
To solve these equations, the first, second and fourth can be used to simultaneously solve for \(f, g, h\). If one is interested in \(p\) then the third expression can be used.
Next, we’ll look at the numerics to solve the system, what the fluid flow looks like the boundary layer and after that, we’ll start on the chemistry that is happening at the interface and how it interacts with the motion of the fluid. We have tacitly assumed that the disk has an infinite radius or effectively infinite since we are neglecting edge effects. If you are interested in what happens for a finite disk then look at the paper by Brady and Durlofsky.
References
Brady, J.F. and Durlofsky, L., (1987). On rotating disk flow, Journal of Fluid Mechanics, 175(1), pp. 363-394.
Levich, V.G. and Spalding, D.B., (1962). Physicochemical hydrodynamics, Prentice-Hall Englewood Cliffs, NJ.
Von Karman, T. and Lin, C.C., (1961). On the existence of an exact solution of the equations of Navier-Stokes, Communications on Pure and Applied Mathematics, 14(3), pp. 645-655.
Zandbergen, P.J. and Dijkstra, D., (1987). Von Karman swirling flows, Annual review of fluid mechanics, 19(1), pp. 465-491.